Abstract
Obtaining a burning plasma is a critical step towards self-sustaining fusion energy1. A burning plasma is one in which the fusion reactions themselves are the primary source of heating in the plasma, which is necessary to sustain and propagate the burn, enabling high energy gain. After decades of fusion research, here we achieve a burning-plasma state in the laboratory. These experiments were conducted at the US National Ignition Facility, a laser facility delivering up to 1.9 megajoules of energy in pulses with peak powers up to 500 terawatts. We use the lasers to generate X-rays in a radiation cavity to indirectly drive a fuel-containing capsule via the X-ray ablation pressure, which results in the implosion process compressing and heating the fuel via mechanical work. The burning-plasma state was created using a strategy to increase the spatial scale of the capsule2,3 through two different implosion concepts4,5,6,7. These experiments show fusion self-heating in excess of the mechanical work injected into the implosions, satisfying several burning-plasma metrics3,8. Additionally, we describe a subset of experiments that appear to have crossed the static self-heating boundary, where fusion heating surpasses the energy losses from radiation and conduction. These results provide an opportunity to study α-particle-dominated plasmas and burning-plasma physics in the laboratory.
Similar content being viewed by others
Main
Fusion research fundamentally aims to create a system that produces more energy than was required to create it, a necessary condition for energy applications; in practice, the fusion reaction must be self-sustaining, with self-heating overtaking loss mechanisms, termed ‘ignited’9. Such conditions are reached in astrophysical objects including the cores of stars, novae and type 1a supernovae, and in thermonuclear weapons. Ignition in the laboratory requires heating the fuel to incredibly high temperatures, where it becomes a ‘plasma’ and fusion reactions readily occur, while also controlling energy losses. Several approaches have been developed to heat and confine plasma over the past several decades, with most pursuing deuterium–tritium (DT) fuel, which most easily achieves ignition. The dominant approaches to plasma confinement are ‘inertial’, an impulsive burn while the fuel is confined by its own inertia, and ‘magnetic’, in which specialized configurations of magnetic fields provide confinement to the charged particles in the plasma. In order for a DT fusion (D + T → α (3.5 MeV) + n (14 MeV)) plasma to become thermally unstable and ignite, it must first obtain a ‘burning’ state. In this regime, self-heating from α-particle deposition exceeds the external heating input into the DT8; this ratio is denoted Qα, where the self-heating is taken relative to the heating power to the plasma—for inertial fusion this is the PdV compressional work on the fuel and not the total laser energy (P, pressure, dV, volume change). Qα > 1 is a burning plasma.
A burning-plasma state signifies a transformational change to the energy and power balance in the DT plasma, opening up the potential for rapidly increasing performance. In the impulsive case of inertial confinement fusion (ICF)10, Qα can be stated either as a power during burn, or as an energy integrated over the burn duration, whereas for the near-steady-state operation of magnetic fusion energy (MFE), Qα is a statement of power. As α-particles carry 1/5 of the total fusion energy per D + T reaction, Qα = Q/5, where Q is the total fusion energy compared to the heating energy supplied. (Or in the MFE case, stated in terms of total fusion power over heating power; for example, the goal of ITER11 is to reach Qα ≈ 2 (Q ≈ 10), whereas the record from the JET tokamak12 is Qα ≈ 0.13 (Q ≈ 0.67).)
A burning plasma is distinct from other scientific milestones in inertial fusion. In 2014, the first milestone of ‘fuel gain’13 (Gfuel > 1) was achieved14, in which the fusion yield exceeds the energy delivered to the fuel; this corresponds to approximately 12–14 kJ of yield at the National Ignition Facility (NIF). At 20–22 kJ, the yield was approximately doubled by self-heating feedback, termed ‘α-heating’15. The next scientific milestone is a burning plasma, as described previously; this is the scientific milestone achieved in this work. No net energy gain, G, relative to the laser energy is expected for a burning plasma. Because of energy losses incurred in achieving the required compressed state, ICF implosions must achieve ignition before a net energy gain is possible. A net energy gain would require fusion yields greater than the laser energy, 1.9 MJ. Although short of ignition or energy gain, a burning plasma (Qα > 1) is a new physics regime for laboratory fusion1,11,16. Studying burning plasmas will elucidate other new physics in this regime, such as self-heating-driven instabilities or kinetic effects in the plasma, which probably depend on the confinement approach.
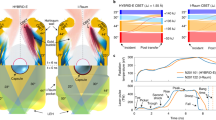
In a tokamak, the predominant approach to magnetic confinement, once the plasma discharge is generated by resistive heating, external power sources, such as radio-frequency antenna, provide additional plasma heating as the plasma is brought to fusion conditions. In indirect-drive ICF, the way energy is delivered to the fusion fuel is different and much less direct. At NIF17, 192 lasers deliver up to 1.9 MJ of frequency-tripled light into a high atomic number (Z) ‘hohlraum’ (Fig. 1) that serves the purpose of an X-ray converter generating a nearly Planckian X-ray bath, an approach known as ‘indirect drive’18. The incident beam-by-beam laser pointing and power in time are designed6 to generate a specific radiation temperature (Trad) history (Fig. 1, bottom left) inside the hohlraum, with sufficient uniformity in a way that is matched to specifics of the target geometry and the desired final plasma state. The exposed surface of a capsule at the centre of the hohlraum absorbs approximately 10–15% of the X-rays, causing the outer edge of the capsule (the ablator) to ionize, generate high pressures of the order of hundreds of Mbar (1 Mbar = 1011 Pa), and expand away from the capsule—a process termed ablation. A shell of cryogenic DT fuel is layered against the inside surface of the ablator, which is in partial-pressure equilibrium with DT vapour in the centre of the capsule (Fig. 1, top left). The inwardly directed acceleration caused by the ablation drives the capsule and DT fuel inwards upon itself (an implosion, shown schematically at the right of Fig. 1) with enormous acceleration (about 1014 m s−2) obtaining velocities of approximately 350–400 km s−1 in a matter of nanoseconds. Most of the X-ray energy (about 92–95%) absorbed by the capsule is consumed by the ablation process, but as a result the DT fuel obtains considerable (about 10–20 kJ) kinetic energy inside a very small volume.
Centre, A typical indirect-drive target configuration with key engineering elements labelled. Laser beams (blue) enter the hohlraum through laser entrance holes at various angles. Top left, A schematic pie diagram showing the radial distribution and dimensions of materials in diamond (high-density carbon, HDC) ablator implosions. Bottom left, The temporal laser power pulse-shape (blue) and associated hohlraum radiation temperature (green). Right, At the centre of the hohlraum, the capsule is bathed in X-rays, which ablate the outer surface of the capsule. The pressure generated drives the capsule inward upon itself (an implosion) which compresses and heats the fusion fuel during the implosion process.
Shortly after the DT fuel acquires peak kinetic energy, the pressure (P) inside the implosion rises markedly, to levels of many hundreds of Gbar (1 Gbar = 1014 Pa), as kinetic energy is converted into internal energy in the DT (a process termed stagnation). An ICF implosion is a pressure amplifier, sacrificing absorbed energy to achieve high energy density and central pressures that are factors of thousands higher than the pressure at the ablation front. The high central pressure is necessary because only a small fraction of the energy at NIF can ever be coupled into the DT fuel, and heating a large mass of DT fuel is energetically costly, as reflected in the heat capacity of DT, cDT = 115 kJ mg−1 keV−1 (9.9 × 103 J kg−1 K−1). In these experiments the total fuel mass is approximately 200 μg and the hot-spot mass is approximately 20–30 μg. As a high ion temperature (Ti) is also needed for fusion, while the fuel stagnates at the centre of the implosion, the DT forms a hot spot from the fuel’s inner surface and PdV work is done on the hot spot, generating very high ion and electron temperatures in near thermal equilibrium (Ti ≈ Te ≈ 4–5 keV, 1 keV = 1.16 × 107 K, where Ti and Te are the ion and electron temperatures). If the conditions of high temperature and pressure are achieved, the hot spot initiates copious DT fusion reactions and self-heating further increases Ti.
ICF experiments have already demonstrated considerable fusion performance enhancement from self-heating14,15, and more recent advances19,20,21 have generated experiments with approximately 50 kJ fusion yields that were close to the burning-plasma threshold3. These experiments used capsules with similar inner radii, between 0.91 and 0.95 mm. Within the maximum laser energy NIF can deliver, these previous designs were limited in the energy coupled to the capsule, and thus in the fuel kinetic energy, by the ability to control the symmetry of the radiation environment within the hohlraum, primarily because an ablated plasma bubble expands from where the outer beams hit the wall (Fig. 1), intercepting the inner beams and thereby suppressing drive at the hohlraum waist22,23. Two tactics have been used to enable symmetry control with more efficient hohlraums driving larger capsules: adjusting cross-beam energy transfer between the outer to inner beams4,24,25 by changing the laser wavelength separation (Δλ); and incorporating a pocket in the hohlraum wall at the outer beam location to delay the bubble propagation5. These tactics have been used to design higher-efficiency hohlraums that control symmetry; we use these hohlraums to drive capsules that are about 10% larger than prior experiments to realize the strategy for achieving a burning plasma laid out in a previous work2. These experimental campaigns are known as ‘Hybrid E’ and ‘I-Raum’; the Hybrid-E campaign uses Δλ exclusively, whereas I-Raum uses a combination of the pocket and Δλ. Key data and analysis supporting this burning-plasma analysis are given in complementary papers: Ross et al.7 (experiments) and Kritcher et al.6.
Four experiments with these new designs have been conducted that have generated record performance at NIF, with triple the fusion yield compared to past experiments4,19,21, to a maximum of approximately 170 kJ reported here. The experiments are referred to by an experiment number denoting the date of the experiment (for example, in the format NYYMMDD, where YY = year, MM = month and DD = day). N201101 and N210207 were experiments using the Hybrid-E platform, and N201122 and N210220 were experiments using the I-Raum platform. The experiments in November (N201101 and N201122) achieved much higher performance relative to past work owing to their increased scale and favourable implosion design parameters, yet each suffered from low-mode degradations; these low-mode asymmetries were mitigated on the subsequent experiments (N210207 and N210220), resulting in higher performance6,7.
On each NIF experiment a comprehensive suite of optical, X-ray and nuclear diagnostics measure key aspects of the implosion performance. Key data are shown in Extended Data Table 1: the total fusion yield in kJ, ion temperature (Ti, measured from DD reactions)7, hot-spot volume and burn width in ps. For a full description of the experimental data and changes between the experiments, see ref. 7. Analytic models using these data are used to infer characteristics of the implosion process and hot spot including the pressure, hot-spot internal energy, implosion velocity and peak kinetic energy in the fuel during implosion, PdV work done on the hot spot, and areal density of the hot spot in g cm−2. These quantities are required to evaluate the burning-plasma criteria. Most of these inferences are described in a previous work26 and Methods; the implosion velocity (vimp) can be inferred from the time of maximum neutron output (‘bang time’) and an implosion dynamics ‘rocket model’ that is calibrated to near-neighbour surrogate experiments in which the implosion trajectory is tracked radiographically27,28.
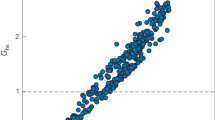
Although it would be desirable to have a direct measure that indicates a burning plasma, such a measurement is not yet known to exist, so inferences from data must be used instead. Gfuel has a direct connection to ignited fusion requirements and suggests a simple metric for assessing a burning plasma from Gfuel = Y/EPdV,tot, where Y is the fusion yield and EPdV,tot is the total PdV work on the fuel (see Methods for how this quantity is evaluated). Figure 2a (also Extended Data Table 1) shows a plot of Gfuel data from many DT implosions at NIF versus the product PT1.6τ, where τ is a confinement time; this is a Lawson-like criterion applicable for Gfuel (Methods).
a, Total fuel gain versus Lawson-like parameter; Gfuel > 5 corresponds to the burning-plasma regime. b, Probability distributions for Gfuel for high-performing experiments. In these plots the width of the shaded region is proportional to the probability distribution and the solid lines mark the 16th, 50th and 84th percentiles of the distribution c, Total α-heating energy versus fuel kinetic energy, Eα/KEfuel > 1 corresponds to Qα > 1. d, Probability distributions in Eα/KEfuel criteria for high-performing experiments. Error bars in a, c are 1 standard deviation (s.d.) and are shown only for the I-Raum and Hybrid-E points. Historical data are from refs. 4,14,15,19,20,21,29,30,31.
As can be seen in Fig. 2a, most experimental series show a linear trend between Gfuel and \(P{T}_{{\rm{i}}}^{1.6}\tau \) and have Gfuel ≤ 5; however, the Hybrid-E and I-Raum implosion series show a transition to a super-linear trend between Gfuel and \(P{T}_{{\rm{i}}}^{1.6}\tau \) (as expected when self-heating exceeds the hot-spot internal energy) and have Gfuel > 5. The non-burning-plasma regime is denoted by the grey shaded region (Gfuel < 5). In this and the following figures, historical data from NIF are shown from refs. 4,14,15,19,20,21,29,30,31, labelled by the names of those predecessor campaigns.
Figure 2b shows the probable distribution of the Gfuel values plotted in Fig. 2a, with the probability distribution in the inferred data quantities included to evaluate the uncertainty (Methods). For comparison, we include a set of previous high-performing NIF experiments from refs. 4,19,21. The abscissa of Fig. 2b are NIF experiment numbers; although several experiments in years prior to November 2020 came very close to the threshold of Gfuel = 5, only the experiments reported here have so far clearly surpassed it (see Extended Data Table 1 for values, where the quoted likelihood is the fraction of the distribution above the threshold).
Alternatively, comparing the total energy produced in α-particles, Eα = Y/5, to the peak kinetic energy of the DT fuel, KEfuel (Fig. 2c), is another simple metric. Similar to Fig. 2b, Fig. 2d shows the probable range of Eα/KEfuel, with normally distributed uncertainties in the input data versus experiment number for the eight highest performing DT experiments at NIF, where again only these four experiments clearly exceed Eα/KEfuel > 1 (see Extended Data Table 1 for values). Because indirect-drive implosions have a small fraction of ablator mass remaining at peak velocity it is important to point out that KEfuel is not the total implosion kinetic energy at peak velocity; instead, because the stagnating shell is compressible and extended radially, only a fraction of the kinetic energy of the ablator can be converted to internal energy before peak burn and disassembly.
Although Gfuel and Eα/KEfuel are suggestive metrics for an ICF burning plasma, two more rigorous and more stringent metrics already exist in the literature3,8. The burning-plasma statement that ‘α-deposition is the dominant source of plasma heating’ is complicated by the temporal nature of an implosion, where the PdV work on the hot spot that does the heating comes before the time of peak fusion rate, a consideration that is not analogous to MFE. Prior works by Hurricane et al. gave a condition on velocity (vcond)2,3 relative to the plasma conditions, which we slightly modify (Methods) to:
in units of keV, g, cm and s. Here, ρRhs is the hot-spot areal density and ⟨σν⟩ is the fusion reactivity.
To evaluate the Hurricane metric, the temperature and areal density of the hot spot, and the implosion velocity, are needed (Methods). The thermonuclear reactivity ⟨σν⟩ is a function of the hot-spot conditions, specifically the temperature; we use the ⟨σν⟩ evaluation of Bosch and Hale32. Figure 3a shows the experiments in hot-spot temperature and areal density parameter space. Previous experiments are shown as points, and the present four experiments are shown as full probability distributions (red, N201101; blue, N201122; purple, N210207; grey, N210220), with contours enclosing 80% of the distribution. In Fig. 3a a single contour of equation (1) for vimp = 385 km s−1, representative of these experiments, is shown. When evaluating the criteria for the actual inferred velocity of each experiment, with uncertainty, is used. These are the first experiments to exceed the Hurricane criterion, as clearly shown by the probability distributions in Fig. 3b. The likelihood of these four experiments exceeding the criteria is 89% (N201101), 79% (N201122), and 100% for both N210207 and N210220.
a, Criteria on temperature and hot-spot ρR established by Hurricane et al.3. Previous experiments are shown as points, and the present four experiments are shown as full probability distributions (red, N201101; blue, N201122; purple, N210207; grey, N210220), with contours enclosing 80% of the distribution. A single contour of equation (1) for vimp = 385 km s−1 is given by the solid black line. b, Probability distribution for experiments exceeding the Hurricane criterion, >1 is a burning plasma. c, Criteria on α-heating and PdV work from a previous work8, including estimates from data inferences (solid symbols) and from 2D simulations (open symbols). d, Probability distribution for experiments exceeding the Betti criteria. For these experiments distributions are shown for data-inferred EPdV,hs (blue) and using 2D simulations (orange). Error bars in a, c are 1 s.d. and are shown only for the I-Raum and Hybrid-E points. Historical data are from refs. 4,14,15,19,20,21,29,30,31.
Equation (1) should be roughly equivalent to the burning-plasma criteria found by Betti et al. (3.5× yield amplification and 0.5Eα/EPdV,hs > 1)8, but for completeness we use both. The first criterion by Betti et al., Yamp ≥ 3.5, is satisfied by our inferred yield amplifications given in Extended Data Table 1, inferred with the prescription in ref. 26 and from two-dimensional (2D) simulations6 using HYDRA33. Two quantities are required to evaluate the second Betti et al. burning-plasma metric. The α-deposited energy (Eα) is straightforward as it is simply 20% of the measured total fusion yield (given in Extended Data Table 1), which is approximately 20 kJ for the first two experiments, about 33 kJ for N210207, and about 31 kJ for N210220. The second input for these criteria is the PdV work done upon the hot spot, which must be inferred; however, such inferences are prone to large uncertainties in the presence of considerable α-heating and bremsstrahlung X-ray losses. We perform this inference in two ways (Methods), first using an analytic hydrodynamic piston model34 of an implosion, and second by extracting PdV work from the 2D radiation–hydrodynamics simulations that best match the experimental observables described in ref 6. These two estimates are used to estimate a range in hot-spot PdV work, and are both plotted in Fig. 3c compared to previous experiments at NIF, with a 1–1 line to denote the burning-plasma regime (above the line). Probability distributions for the metric quantity itself are shown in Fig. 3d. From Betti’s criteria, with the experimental (simulated) EPdV,hs, we assess that 74% (0%) and 97% (2%) probability for experiments N201101 and N201122, respectively, are in the burning-plasma regime. The difference in probability reflects the fact that the simulated PdV work is higher and thus is more pessimistic for satisfying the criteria, with the simulated values for these experiments being below the burning-plasma threshold. With improved performance, experiments N210207 and N210220 are assessed to be in the burning-plasma regime with 100% confidence by both experimental and simulated methodologies. These correspond to an an inferred Qα ≈ 1.4–1.6 for experiment N210207, and Qα ≈ 1.3–2.0 for experiment N210220.
Several metrics for assessing whether these implosions created a burning-plasma state have been discussed and presented in Extended Data Table 1 and Figs. 2, 3. In each case, burning-plasma likelihoods are calculated by propagating uncertainties in each quantity through the metric (Methods), shown in the figures with likelihood values discussed and summarized in Extended Data Table 1. Quantitatively, we see that the first two (N201101 and N201122) are probably in the burning-plasma regime by all metrics, except Betti’s, when evaluated with the simulated EPdV,hs; the most recent experiments (N210207 and N210220) are overwhelmingly likely to have passed this threshold. Qualitatively, our confidence in this conclusion is further increased by the use of multiple independent metrics.
The achievement of a burning-plasma state is key progress towards the larger goal of ‘ignition’ and overall energy gain in inertial fusion. The fusion yields reported here (approximately 0.17 MJ) are lower than the input laser energy (approximately 1.9 MJ), but are nearly equal to the capsule absorbed energy (giving capsule gain of about 0.7–0.8) and are an order of magnitude greater than the input energy transferred to the fusion fuel. Moreover, the total fusion power (5mPα where Pα is the power per unit mass) generated in the two highest performing experiments are at petawatt levels (for example, approximately 1.6 ± 0.2 PW for N210207).
In the burning-plasma regime, self-heating can overtake loss mechanisms, which include bremsstrahlung losses, thermal conductivity and negative PdV work upon expansion. Simple expressions for the power-balance terms are given in the Methods and values for the four experiments are given in Extended Data Table 1. Here, we use a bremsstrahlung enhancement factor fb ≈ 1.15 that is inferred from the data35. The first two experiments have self-heating comparable to the radiation losses. An important new regime is when self-heating power (Pα) is greater than both the radiation (Pb) and conduction losses (Pe)—that is, fαPα > Pb + Pe, where fα is the fraction of α-particles stopping in the hot spot36. A contour for this regime is shown in Fig. 3a by the black dashed line. Experiment N210220 is close to entering this regime, and we infer that experiment N210207 has entered this regime with 82% likelihood. The level of α-heating in this work is still short of that required for ignition.
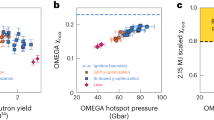
To achieve ignition—defined as a yield amplification (Yamp ≈ 20–30) consistent with about 1 MJ fusion yield37, and then high gain—further progress is needed. Figure 4 shows these experiments in the larger context of ignition, in the parameter space of hot-spot pressure and energy (Fig. 4, left) and in yield amplification versus a Lawson-like parameter called the ‘ignition threshold factor’ experimentally inferred (ITFX)8,26,38 for conditions without α-heating (nα) (Fig. 4, right). Figure 4, right, plots this quantity as \({{\rm{ITFX}}}_{{\rm{n}}{\rm{\alpha }}}^{0.34}\), which is approximately equivalent to χnα as defined previously8. Proximity to ignition can be gauged qualitatively in terms of the product P2Ehs (equivalent to (ρRhsTi)3), or in terms of ITFXnα or χnα ≈ 1, representing ignition. Figure 4, left, shows contours of P2Ehs relative to N210207, showing that this metric has been improved by a factor of several from previous results. From Fig. 4 we clearly see that these four experiments are the closest to ignition, but a further increase in ITFXnα from approximately 0.6 → 1 is required. As this Article was being finalized, a new experiment in this series on 8 August 2021 produced approximately 1.35 MJ of fusion yield and capsule gain of approximately 5, breaking all previous records. This was announced by our institution in a press release39; this experiment will be described in a future publication.
Left, hot-spot pressure and energy. The product P2Ehs is representative of proximity to ignition; contours of this metric relative to N210207 are shown by the dashed grey curves. Right, yield amplification (Yamp) versus ITFXnα. These are the highest performing ICF experiments so far and the closest to ignition. The inset shows these experiments in detail with both inferred (solid) and simulated (open) Yamp. Error bars are 1 s.d. and are shown only for the I-Raum and Hybrid-E points, plus shot N180128. Historical data are from refs. 4,14,15,19,20,21,29,30,31.
As discussed in the complementary papers6,7, these experiments have clear and specific degradation mechanisms, which can be mitigated for further improvement in performance. More generally, the ICF programme at NIF is pursuing several approaches that can enable additional progress: reducing degradation mechanisms including low-mode asymmetry40,41,42 and radiative losses from mix35, further increasing energy coupled to the capsule4,43, and improving compression of the fuel44.
In conclusion, we have generated in the laboratory a burning- plasma state in which the plasma is predominantly self-heated. This was accomplished using inertial fusion implosions at the US NIF; previous experiments here were just below the threshold for a burning plasma. We increased the capsule scale relative to previous work, increased the coupling efficiency from laser energy to the capsule, and controlled implosion symmetry using new tactics. Four experiments have been conducted that have passed the threshold for a burning plasma by several metrics, with especially high confidence on the most recent two experiments. Additionally, the highest performing experiment (N210207) is in a more stringent regime where the self-heating surpasses energy losses from radiation and conduction. Although these results are short of total energy gain from the system owing to the inherent inefficiencies of ICF, these experiments represent a substantial step towards this goal with record values of parameters that assess our proximity to ignition at NIF. Several promising avenues for further increases in performance are identified and will be pursued by the US inertial fusion programme, in addition to novel physics in the burning-plasma regime such as α-particle-driven processes.
Methods
Terminology
Definitions of commonly used mathematical symbols are summarized in Extended Data Table 2.
Reproducibility
Experiments subsequent to those described in this Article have demonstrated the reproducibility of a burning-plasma state at NIF, with two additional experiments that have performance comparable to the highest-performing experiments in this Article. These newer experiments, N210307 and N210605, were conducted in the Hybrid E platform. N210307 repeated N210207, albeit using a capsule from a different fabrication batch and produced a yield of approximately 145 kJ with an experimentally inferred Qα = 1.34 ± 0.07 from the Hurricane criterion. Experiment N210605 reduced the thickness of the ice layer relative to N210207 and resulted in a lower yield (135 kJ) but high ion temperature, with Qα = 1.40 ± 0.10, again from the Hurricane criterion. These additional experiments confirm that the burning-plasma state is reproducible at NIF, and full details and analysis on them will be presented in future publications.
Inferred hot-spot conditions
Hot-spot conditions must be inferred from measured quantities using a model. The simplest hot-spot model is to assume an isobaric volume of uniform conditions, as used in a previous work14 between equations 2 and 3, in which case the hot-spot number density is given by
where Y is the fusion yield in J, ⟨σν⟩ is the fusion reactivity, which depends on the ion temperature (Ti), Vhs is the hot-spot volume in cm3, and τ is the burn duration in s, for equimolar DT mixtures. The remaining hot-spot quantities follow from the inferred density, including the pressure (P = (1 + Z)nkBTi, with kB Boltzmann’s constant), hot-spot energy (Ehs = 1.5PVhs), and areal density \(({\rho R}_{{\rm{h}}{\rm{s}}}=(2.5n/{N}_{{\rm{a}}})\sqrt[3]{3{V}_{{\rm{h}}{\rm{s}}}/4\pi })\).
A more detailed inference is to use a one-dimensional (1D) profile in radius for temperature and density, maintaining the isobaric assumption. A conduction-limited profile follows the expression45:
where Tmin is the temperature at the boundary, T0 is the central temperature and R0 is the hot-spot boundary. β is the thermal conductivity power law, 2.5 from classical Spitzer conductivity. Following a previous work26 we use a lower value, β = 2/3, which accounts for additional physics, dynamical processes and reproduces radiation–hydrodynamics simulations. The density profile is then determined by the isobaric assumption through P ∝ nT being constant. Tmin is taken as 1 keV leaving T0, R0 and P as free parameters in the model; the data are compared to synthetic data calculated from this 1D profile with the model parameters adjusted to minimize residuals. As in the zero-dimensional (0D) model, the hot-spot energy simply follows from pressure and volume, and the areal density is the mass density integrated over the inferred radial profile.
In either dimensionality the model’s radius is matched to the experimental measurements, which take a contour of emission level, by calculating synthetic emission images to calculate an equivalent contour radius. The measurements include 2D and three-dimensional (3D) asymmetries, so an equivalent spherical volume, and radius, are calculated using the modal decompositions, where the emission contour measured from the equator (Req) and pole (Rpo) are
where P0 and M0 are the average measured sizes from each view, δPℓ (δMm) is the relative modal amplitude, often referred to as Pℓ/P0 with the nomenclature above chosen for clarity. Pℓ are the Legendre polynomials, and ϕm are the orientation of the azimuthal modes. Rhs is the hot-spot radius as a function of both θ and ϕ, which is integrated to obtain the volume. Here, the dominant parameters are P0, M0 and δP2, which are given in ref. 7.
Implosion velocity (vimp) is inferred using a rocket model of the implosion46 constrained by both supporting experiments, especially in-flight radiography, and the measured time of peak nuclear production on each experiment. The inferred yield amplification given in Extended Data Table 1 is a function of the measured yield, shell compression and fuel mass (mfuel); both the velocity and Yamp inferences use the prescription given in a previous work26. The fuel kinetic energy then follows from \(\frac{1}{2}{m}_{{\rm{fuel}}}{v}_{{\rm{imp}}}^{2}\). Our techniques for inferring the PdV work done on the fuel are discussed in the following section.
A comparison of inferred values using 0D and 1D models are shown in Extended Data Table 3. Inferred pressures are highly consistent between these calculations, whereas hot-spot energies and areal densities are higher in the 1D model owing to substantial mass near the 1 keV temperature cut-off.
Inferring G fuel
The total fusion yield produced by a mass (m) of DT, over a characteristic confinement time, τ, is Y ≈ 5mPατ—with Pα = 8.2 × 1024ρ⟨σν⟩ in GJ g−1 s−1 the specific DT fusion power for a given mass density, ρ, of DT with reaction rate ⟨σν⟩—and the internal energy in that DT is Ehs = cDTmTi. Therefore, one can write (O.A.H. et al., manuscript in preparation)
with
where P is in Gbar, Ti in keV, and τ in s. In equation (7), the total energy delivered by PdV work, EPdV,tot, is determined from the hot spot and compressed, but cold, DT fuel energy at stagnation, Ehs and Efuel, respectively, at peak compression. The last term in the denominator represents a correction for additional energy retained by self-heating of the fuel from α-particle deposition but not then lost as bremsstrahlung. So, EPdV,tot ≈ Ehs + Efuel − qY/10, where q is a ‘quality’ factor, 0 ≤ q ≤ 1, measuring the ability of the implosion to retain self-heating energy (O.A.H. et al., manuscript in preparation). Here we use q ≈ 0.7, inferred from simulations, and the factor of 10 results from one-fifth of the fusion energy released as α-particles and half of those produced up until the time of peak fusion burn. Albeit generally arrived at in a different fashion than above, the product P(⟨σν⟩/T2)τ is Lawson’s9 parameter for ignition. Figure 2a uses the useful reaction-rate approximation \(\langle \sigma v\rangle \approx 4.2\times {10}^{-20}{T}_{{\rm{i}}}^{3.6}\) (in units of cm3 s−1 for ion temperature range 3.5 < Ti < 6.5 keV) to simplify the abscissa.
An expression for the fuel gain is given in equation (7). The yield is measured and the hot-spot energy is inferred as described in the previous section. Precisely determining the cold-fuel energy from data is not straightforward. For the purposes of this analysis we actually require the total PdV work done on all the DT. This is at a minimum the fuel kinetic energy and internal energy at peak velocity, which are both inferred. This neglects any work done by the inflowing remaining ablator material on the fuel, which can occur in these implosions. In this case the hot-spot energy is more than half the previous estimate; in this scenario we assume equipartition between the hot spot and cold fuel to evaluate equation (7).
Inferred PdV work
The primary uncertainty in the Betti metric8 is in the inference of PdV work on the hot spot. Here we use three methodologies: two inferences using an analytic model, and a direct extraction of PdV work from simulations that match the experimental observables.
We use the hydrodynamic piston model of an implosion described previously34. This analytic model abstracts the implosion process using opposed pistons to represent the imploding shell. In spherical geometry, the stagnation pressure from this mechanical work on the hot spot is given by (equation 24in ref. 34):
where ρδRave is the average shell areal density, calculated from the measured neutron ‘down-scattered ratio’ (DSR) using the relation ρδRave ≈ 19.3DSR, vimp is the implosion velocity and Rhs is the average hot-spot radius (which can be obtained from the volume, Vhs, given in Extended Data Table 1). The factor f 2 represents the effect of mode-1 asymmetry and is a measure of the residual kinetic energy (kinetic energy that is never converted into internal energy) in the implosion.
From the piston pressure we obtain the hot-spot internal energy (Ehs) from
In the absence of α-heating (which adds energy to the hot-spot) and radiative X-ray losses, or when α-heating exactly balances X-ray losses, then Ehs = EPdV,hs. For low yield amplification implosions (Yamp < 1.5), X-ray losses dominate over α-heating energy gains, so Ehs < EPdV,hs. For higher yield amplification implosions (Yamp > 2), α-heating energy gains start to dominate over X-ray losses, so Ehs > EPdV,hs. The estimated values for these four experiments are given in Extended Data Table 4 as the piston methodology.
We can also estimate the stagnated fuel mass in a similar fashion, using
which allows us to then estimate the total mass that stagnates from mshell + mhs, with mhs from the hot-spot inferences described earlier. We then estimate the PdV work from
where mfuel is the initial fuel mass. The factor of 0.73 is derived from 1D simulations in which the imploding mass stagnates efficiently, and we drop the residual kinetic energy factor f 2 because the inferred shell mass does not include non-stagnated material. This estimate leads to smaller estimates of EPdV,hs than the first empirical estimate, and are given in Extended Data Table 4 as the stagnated mass estimate.
For analysis of previously published campaigns we use the simple relation EPdV,hs ≈ (0.5–0.7)KEfuel(1 − f 2), this is easy to evaluate with the available data and the factor 0.5–0.7 accounts for a wide range of 1D to 2D/3D behaviour observed on past experiments. For comparison, the proportionality constant inferred from the first methodology (equation (10)) is between 0.60 and 0.73 for our four experiments.
We also use radiation–hydrodynamics simulations to estimate the PdV work done on these implosions. The first simulation-based methodology is to use 2D simulations with degradation mechanisms that match the observed performance, and interrogate the work done upon the mass elements that form the hot spot to infer EPdV,hs. The simulation methodology is described in ref. 6, and the values of EPdV,hs for this method are given in Extended Data Table 4. The same fusion performance can be generated with varying application of degradation mechanisms that either degrade EPdV,hs or do not; an estimate of the 2D simulation uncertainty of ±0.5 kJ is estimated by studying multiple simulations.
A similar energy-balance analysis can be done with 1D simulations, in which the work done upon the hot spot is well defined with a Lagrangian mesh. The 1D simulations are tuned to match the measured yields, but are expected to underestimate EPdV,hs since they cannot properly incorporate residual kinetic energy. This estimate is given in Extended Data Table 4 as an upper bound.
We have thus develop four methodologies for estimating EPdV,hs. In the main analysis we use a combination of the empirical piston model estimate as the more pessimistic data-based inference, and use the 2D simulated EPdV,hs as the most robust computational description of the experiments.
Modified Hurricane metric
At peak burn, the time rate of change of hot-spot volume, dV/dt, is nearly zero, and therefore so is the heating rate, so time integration is needed. Mathematically, a statement of a burning plasma appropriate for ICF is
where tpf is the time of peak fusion rate, and tminV is the time of minimum hot-spot volume.
The integrals in equation (13) are easily approximated2 without knowing the details of the actual implosion using the mathematical method of steepest descent; assuming that the thermodynamic quantities of interest, such as T, P, ρ, and so on, are impulsive, being highly peaked around the time of stagnation. Ultimately, the solution to equation (13), in terms of only burn-average hot-spot areal density, ρRhs, Ti and vimp is equation (1) after a correction to the original derivation.
A recent note from our colleagues at Los Alamos47 discovered an arithmetic error in the derivation of the criteria as published in ref. 3. The error is in going from equation 8 to equation 9 in ref. 3, in which the conversion to peak temperature (T0) to burn-averaged temperature (Ths) should be, for n ≈ 4,
Additionally, we now believe that the inclusion of the fraction of α-particles stopping in the hot spot (fα) in ref. 3 was inappropriate. When considering the temperature evolution of a defined mass—for example, the self-heating criterion in equation (17)—this is necessary because fα is fundamentally the fraction of α-particle energy deposited into that mass. On the other hand, the burning-plasma criteria is one on the energy of the hot spot,
and α-particles that escape the hot spot still contribute to its energy via generation of additional hot-spot mass, as seen by examining the time derivative of the above:
Therefore, the inclusion of fα in a burning-plasma criterion is inappropriate. We note that not including an fα factor is consistent with other criteria, for example, ref. 8. With these two modifications to the criterion published in ref. 3 we use a new criterion (equation (1)). This modified criterion is slightly more restrictive for the burning-plasma threshold in the regime relevant to these experiments.
Model uncertainties for Hurricane’s metric
The Hurricane metric3 depends on more quantities than the Betti metric, although these quantities are more straightforward to infer than EPdV,hs. The metric reduces to equation (1) where ρRhs and vimp are inferred as described previously, and Ti is measured. ⟨σν⟩ contains some systematic uncertainty from the evaluation used. Data uncertainties are well defined for Ti and in the inference of ρRhs and vimp, and are propagated as described in the next section; the inferred ρRhs can also vary between models, which will be discussed.
Equation (1) depends on the fusion reactivity; in this work we use the evaluation from Bosch and Hale32. Recent publications have presented alternative evaluations48 which differ by about 2%. We note that the inferred \(\rho R\propto 1/\sqrt{\langle \sigma v\rangle }\) from equation (2), so the condition in equation (1) depends on the reactivity as \(1/\sqrt{\langle \sigma v\rangle }\). fα is also weakly increasing with ρR, leading to the condition being slightly less than square-root dependent on ⟨σν⟩, so this criterion has <1% uncertainty from the choice of ⟨σν⟩ evaluation.
The Hurricane criterion is sensitive to the inferred hot-spot ρR, which can vary between models depending on the spatial dependence of ρ. As shown in Extended Data Table 3, the 0D and 1D hot-spot models agree quite well. We also check these values using a 3D reconstruction of the hot-spot density and temperature profiles (a yet unpublished method of L. Divol, but briefly described in ref. 35): for N201101 this gives a value of ρRhs ≈ 0.36–0.38 g cm−2 to the 1-keV contour for N201101 and ρRhs ≈ 0.35–0.36 g cm−2 for N201122. These values are consistent with the simple models described earlier.
Self-heating regime
The hot-spot per unit mass power balance is:
which describes the temporal evolution of the temperature (T) in terms of the balance of self heating (Pα) versus bremsstrahlung (Pb) and electron conduction (Pe) losses plus PdV work. Here electron conduction losses are calculated relative to a hot-spot boundary that is defined relative to a fraction of the peak burn rate or a specified ion temperature. Thermal conduction cools the hot spot while increasing the mass of the hot spot. Because the fusion burn rate is more strongly dependent on the temperature of the spot than its mass in the temperature range achieved by compression alone, α-heating must provide sufficient heating for the hot-spot temperature to increase in the presence of this conduction into an increasing mass. Hot-spot volume change, dV/dt, is negative on implosion, increasing T. During expansion the PdV term becomes an energy loss term. The bremsstrahlung loss can be enhanced beyond the emission of clean DT by the presence of high-Z contamination of the DT (that is, mix), by a fraction fb. In equation (17), fα is the fraction of α-particles stopped in the hot spot, evaluated using fits with modern stopping-power theory36.
Uncertainty analysis
We perform uncertainty analysis for all hot-spot quantities by propagating the normally distributed uncertainties in measured quantities through the 0D and 1D models described earlier. The model input parameters are those that fully describe the system, and are constrained by the measured yield, ion temperature, burn widths (from both X-rays and γ-rays), and volume from the 17% contour of neutron emissivity. Distributions of model parameters are generated using Markov chain Monte Carlo (MCMC), calculated with the tensorflow49 probability package. The log-likelihood function for MCMC is defined by the measurements and calculated with the log-likelihood function
which is summed over all observables (i) where mi is the model value, yi is the measured value and δyi is the uncertainty in the measurement. This methodology produces full distributions of the model parameters including any correlations, from the model parameter distributions we generate full distributions of all hot-spot parameters, some of which exhibit correlation, such as in the temperature and areal density required to evaluate the Hurricane metric, which are partially anti-correlated (evident in Fig. 3a). Other inferences, such as the implosion velocity or kinetic energy, are treated with normally distributed uncertainties that are uncorrelated with the hot-spot inferences.
Power-balance relations
In evaluating the power-balance relations relevant to equation (17) we use the following expressions for the individual terms:
In these expressions the specific powers are given in units of GJ g−1 s−1 and thus are multiplied by the inferred hot-spot mass to obtain power. ρ is the hot-spot mass in g cm−3, ⟨σν⟩ is the fusion reactivity evaluated as a function of temperature in cm3 s−1, T is the temperature in keV, and ρR is the hot-spot areal density in g cm−2. The self-heating power Pα is multiplied by the fraction of α-particle energy deposited in the hot spot (fα) using the evaluation published in ref. 36; for all four experiments, fα ≈ 0.77–0.80.
Data availability
Raw data were generated at the National Ignition Facility. Derived data supporting the findings of this study are available from the corresponding authors upon request.
Change history
02 February 2022
In the version of this article initially published, there was a typo in the url of reference 39. The error has now been corrected.
16 March 2022
A Correction to this paper has been published: https://doi.org/10.1038/s41586-022-04607-2
References
National Academies of Sciences, Engineering, and Medicine. Final Report of the Committee on a Strategic Plan for U.S. Burning Plasma Research (National Academies Press, 2019).
Hurricane, O. A. et al. Beyond alpha-heating: driving inertially confined fusion implosions toward a burning-plasma state on the National Ignition Facility. Plasma Phys. Control. Fusion 61, 014033 (2019).
Hurricane, O. A. et al. Approaching a burning plasma on the NIF. Phys. Plasmas 26, 052704 (2019).
Zylstra, A. B. et al. Record energetics for an inertial fusion implosion at NIF. Phys. Rev. Lett. 126, 025001 (2021).
Robey, H. F., Berzak Hopkins, L., Milovich, J. L. & Meezan, N. B. The I-Raum: a new shaped hohlraum for improved inner beam propagation in indirectly-driven ICF implosions on the National Ignition Facility. Phys. Plasmas 25, 012711 (2018).
Kritcher, A. et al. Design of inertial fusion implosions reaching the burning plasma regime. Nat. Phys. (in the press).
Ross, J. S. et al. Experiments conducted in the burning plasma regime with inertial fusion implosions. Preprint at https://arxiv.org/abs/2111.04640 (2021).
Betti, R. et al. Alpha heating and burning plasmas in inertial confinement fusion. Phys. Rev. Lett. 114, 255003 (2015).
Lawson, J. D. Some criteria for a power producing thermonuclear reactor. Proc. Phys. Soc. B 70, 6 (1957).
Nuckolls, J., Wood, L., Thiessen, A. & Zimmerman, G. Laser compression of matter to super-high densities: thermonuclear (CTR) applications. Nature 239, 139–142 (1972).
Green, B. & ITER International Team and Participant Teams ITER: burning plasma physics experiment. Plasma Phys. Control. Fusion 45, 687–706 (2003).
Keilhacker, M. et al. High fusion performance from deuterium–tritium plasmas in JET. Nucl. Fusion 39, 209–234 (1999).
Atzeni, S. & Meyer-ter-Vehn, J. The Physics of Inertial Fusion (Oxford Univ. Press, 2004).
Hurricane, O. et al. Fuel gain exceeding unity in an inertially confined fusion implosion. Nature 506, 343–348 (2014).
Hurricane, O. A. et al. Inertially confined fusion plasmas dominated by alpha-particle self-heating. Nat. Phys. 12, 800–806 (2016).
Coppi, B. In Academician A. D. Sakharov. Scientific Works. To His Centenary (eds B. L. Altshuler, et al.) (Fizmatlit, 2021).
Moses, E. I. et al. The National Ignition Facility: transition to a user facility. In 8th Intl Conf. Inertial Fusion Sciences and Applications (IFSA 2013) Vol. 688 012073 (2016).
Lindl, J. Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain. Phys. Plasmas 2, 3933–4024 (1995).
Le Pape, S. et al. Fusion energy output greater than the kinetic energy of an imploding shell at the National Ignition Facility. Phys. Rev. Lett. 120, 245003 (2018).
Casey, D. T. et al. The high velocity, high adiabat, “Bigfoot” campaign and tests of indirect-drive implosion scaling. Phys. Plasmas 25, 056308 (2018).
Baker, K. L. et al. Hotspot parameter scaling with velocity and yield for high-adiabat layered implosions at the National Ignition Facility. Phys. Rev. E 102, 023210 (2020).
Callahan, D. A. et al. Exploring the limits of case-to-capsule ratio, pulse length, and picket energy for symmetric hohlraum drive on the National Ignition Facility Laser. Phys. Plasmas 25, 056305 (2018).
Hopkins, L. B. et al. Toward a burning plasma state using diamond ablator inertially confined fusion (ICF) implosions on the National Ignition Facility (NIF). Plasma Phys. Control. Fusion 61, 014023 (2018).
Michel, P. et al. Symmetry tuning via controlled crossed-beam energy transfer on the National Ignition Facility. Phys. Plasmas 17, 056305 (2010).
Glenzer, S. H. et al. Symmetric inertial confinement fusion implosions at ultra-high laser energies. Science 327, 1228–1231 (2010).
Patel, P. K. et al. Hotspot conditions achieved in inertial confinement fusion experiments on the National Ignition Facility. Phys. Plasmas 27, 050901 (2020).
Landen, O. L. et al. Capsule implosion optimization during the indirect-drive National Ignition Campaign. Phys. Plasmas 18, 051002 (2011).
Meezan, N. B. et al. X-ray driven implosions at ignition relevant velocities on the National Ignition Facility. Phys. Plasmas 20, 056311 (2013).
Baker, K. L. et al. High-performance indirect-drive cryogenic implosions at high adiabat on the National Ignition Facility. Phys. Rev. Lett. 121, 135001 (2018).
Döppner, T. et al. Achieving 280 Gbar hot spot pressure in DT-layered CH capsule implosions at the national ignition facility. Phys. Plasmas 27, 042701 (2020).
Hohenberger, M. et al. Integrated performance of large HDC-capsule implosions on the National Ignition Facility. Phys. Plasmas 27, 112704 (2020).
Bosch, H.-S. & Hale, G. Improved formulas for fusion cross-sections and thermal reactivities. Nucl. Fusion 32, 611–631 (1992).
Marinak, M. M. et al. Three-dimensional HYDRA simulations of National Ignition Facility targets. Phys. Plasmas 8, 2275–2280 (2001).
Hurricane, O. A. et al. An analytic asymmetric-piston model for the impact of mode-1 shell asymmetry on ICF implosions. Phys. Plasmas 27, 062704 (2020).
Pak, A. et al. Impact of localized radiative loss on inertial confinement fusion implosions. Phys. Rev. Lett. 124, 145001 (2020).
Zylstra, A. B. & Hurricane, O. A. On alpha-particle transport in inertial fusion. Phys. Plasmas 26, 062701 (2019).
Christopherson, A. R., Betti, R. & Lindl, J. D. Thermonuclear ignition and the onset of propagating burn in inertial fusion implosions. Phys. Rev. E 99, 021201 (2019).
Spears, B. K. et al. Performance metrics for inertial confinement fusion implosions: Aspects of the technical framework for measuring progress in the National Ignition Campaign. Phys. Plasmas 19, 056316 (2012).
LLNL. National Ignition Facility experiment puts researchers at threshold of fusion ignition. Lawrence Livermore National Laboratory – News https://www.llnl.gov/news/national-ignition-facility-experiment-puts-researchers-threshold-fusion-ignition (18 August 2021).
Rinderknecht, H. G. et al. Azimuthal drive asymmetry in inertial confinement fusion implosions on the National Ignition Facility. Phys. Rev. Lett. 124, 145002 (2020).
Tommasini, R. et al. Time-resolved fuel density profiles of the stagnation phase of indirect-drive inertial confinement implosions. Phys. Rev. Lett. 125, 155003 (2020).
Casey, D. T. et al. Evidence of three-dimensional asymmetries seeded by high-density carbon-ablator nonuniformity in experiments at the National Ignition Facility. Phys. Rev. Lett. 126, 025002 (2021).
Amendt, P. et al. Ultra-high (>30%) coupling efficiency designs for demonstrating central hot-spot ignition on the National Ignition Facility using a Frustraum. Phys. Plasmas 26, 082707 (2019).
Landen, O. L. et al. Yield and compression trends and reproducibility at NIF. High Energy Density Phys. 36, 100755 (2020).
Cerjan, C., Springer, P. T. & Sepke, S. M. Integrated diagnostic analysis of inertial confinement fusion capsule performance. Phys. Plasmas 20, 056319 (2013).
Hurricane, O. A. et al. On the importance of minimizing “coast-time” in X-ray driven inertially confined fusion implosions. Phys. Plasmas 24, 092706 (2017).
Albright, B. et al. Comment on the burning plasma condition of Hurricane et. al [Phys. Plasmas 26, 052704, 2019] and implications for the experimental achievement of a burning plasma state on the NIF. Report No. LA-UR-21-25149 (Los Alamos National Laboratory, 2021).
de Souza, R. S., Boston, S. R., Coc, A. & Iliadis, C. Thermonuclear fusion rates for tritium + deuterium using Bayesian methods. Phys. Rev. C 99, 014619 (2019).
Abadi, M. et al. Tensorflow: a system for large-scale machine learning. In Proc. 12th USENIX Symp. Operating Systems Design and Implementation (OSDI’16) (eds Keeton, K. & Roscoe, T.) 265–283 (USENIX Association, 2016).
Acknowledgements
We thank B. Coppi (MIT), S. C. Cowley (PPPL), D. Whyte (MIT), J. Hammer (LLNL), M. Farrell (GA) and J. Kline (LANL) for discussions. The contributions of NIF operations and target fabrication teams to the success of these experiments are acknowledged. This work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under contract DE-AC52-07NA27344. This document was prepared as an account of work sponsored by an agency of the US government. Neither the US government nor Lawrence Livermore National Security, LLC, nor any of their employees makes any warranty, expressed or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favouring by the US government or Lawrence Livermore National Security, LLC. The views and opinions of authors expressed herein do not necessarily state or reflect those of the US government or Lawrence Livermore National Security, LLC, and shall not be used for advertising or product endorsement purposes. Document release number: LLNL-JRNL-819741-DRAFT.
Author information
Authors and Affiliations
Contributions
A.B.Z. hot-spot analysis lead, Hybrid-E experimental lead, wrote sections of the paper; O.A.H. capsule scale/burning-plasma strategy, theory, 0D hot-spot models, and wrote sections of paper; D.A.C. empirical hohlraum P2 model and hohlraum strategy; A.L.K. Hybrid-E design lead, integrated hohlraum group lead, wrote sections of paper; J.E.R. N201101 and N210207 experimentalist and shot-responsible individual (shot RI); H.F.R. original I-Raum design lead; J.S.R. I-Raum experimental lead and N201122 shot RI; C.V.Y. present I-Raum design lead, wrote sections of paper; K.L.B. Hybrid shot RI; D.T.C. Hybrid shot RI; T.D. Hybrid shot RI; L.D. 3D hot-spot analysis; M.H. Hybrid shot RI; S.L.P. Hybrid shot RI; A.P. Hybrid and I-Raum shot RI, physics of capsule engineering defects; P.K.P. 1D hot-spot analysis, Yamp and GLC inference; R.T. Hybrid shot RI; S.J.A. capsule microstructure physics; P.A.A. hohlraum physics; L.J.A. engineering and targets; B.B. penumbral X-ray diagnostic; D.B. computational physics; L.R.B., C.T. X-ray framing camera; L.B.H. HDC design and campaign lead; R.B. ICF physics/ignition theory; S.D.B. cryo-layering; J.B. capsule fabrication; R.M.B. RTNAD nuclear diagnostic; N.W.B. neutron diagnostics; E.J.B. project engineering; D.K.B. diagnostics; T.B. capsule fab and metrology; T.M.B. cryo-layering; M.W.B. project engineering; P.M.C. DT EOS measurements; B.C. HYDRA code development; T.C. LPI physics; H.C. GLEH X-ray diagnostic; C.C. target fab planning; A.R.C. ignition theory; D.S.C. capsule/instability physics; J.W.C. capsule fabrication; E.L.D. experiments; T.R.D. capsule physics; M.J.E. programme management; W.A.F. hohlraum physics; J.E.F. 2DConA image analysis; D.F. nuclear diagnostics; J.F. magnetic recoil spectrometer nuclear diagnostic; J.G. ensemble simulations; M.G.J. magnetic recoil spectrometer diagnostic; S.H.G. ICF physics; G.P.G. nuclear diagnostics; S.H. capsule physics, iPOM analysis; K. D. Hahn neutron diagnostics; G.N.H. experiments; B.A.H. capsule physics; J.H. computational physics; E.H. nuclear time-of-flight diagnostics; J.E.H. MOR and PAM stability, SSD improvements, and FC control; V.J.H. MOR and PAM stability, SSD improvements, and FC control; H. Herrman gamma diagnostics; M.C.H. programme management; D.E.H. hohlraum physics, CBET studies in Hybrid-C; D.D.H. capsule physics; J.P.H. X-ray diagnostics; W.W.H. management; H. Huang capsule fabrication; K. D. Humbird ensemble simulations; N.I. X-ray diagnostics; L.C.J. X-ray diagnostics; J.J. neutron diagnostics; O.J. hohlraum physics; G.D.K. HYDRA code development; S.M.K. neutron diagnostics; S.F.K. X-ray diagnostics and analysis; J.K. diagnostic management; Y.K. gamma diagnostics; H.G.K. gamma diagnostics; V.G.K. neutron diagnostics; C.K. capsules; J.M.K. HYDRA code development; J.J.K. targets; M.K.G.K. ICF physics; B.K. ensemble simulations; O.L.L. velocity analysis; S.L. laser plasma instability (PF3D) code development; D.L. NIF facility management; N.C.L. optical diagnostics; J.D.L. ICF physics; T. Ma ICF physics; M.J.M. X-ray diagnostics; B.J.M. mode-1 analysis, backscatter; A.J.M. diagnostic management; S.A.M. integrated design physics; A.G.M. X-ray diagnostics; M.M.M. HYDRA code development lead; D.A.M. X-ray diagnostics; E.V.M. X-ray diagnostics; L.M. capsule physics; K.M. gamma diagnostics; N.B.M. advanced hohlraum lead; P.A.M. LPI physics; M.M. optical diagnostics; J.L.M. hohlraum physics; J.D.M. hohlraum physics; A.S.M. neutron diagnostics; J.W.M. hohlraum physics; T. Murphy neutron and gamma diagnostics; K.N. project engineering; J.G.D.N. MOR and PAM stability, SSD improvements and FC control; A.N. target fab engineering, capsule and fab planning; R.N. ensembles simulations; M.V.P. HYDRA code development; L.J.P. MOR and PAM stability, SSD improvement and FC control; J.L.P. ensembles simulations; Y.P. hohlraum physics; B.B.P. hohlraum physics; M. Ratledge capsule fabrication; N.G.R. capsule fabrication; H.R. RTNAD mode-1 analysis; M. Rosen hohlraum physics; M.S.R. X-ray diagnostics; J.D.S. hohlraum physics; J.S. mode-1 analysis; S. Schiaffino capsules; D. J. Schlossberg neutron diagnostics; M.B.S. hohlraum diagnostics; C.R.S. HYDRA code development; H.A.S. NLTE opacities (Cretin) code development; S.M.S. HYDRA code development; K.S. mode-1 metrology; M.W.S. kinetic physics; S. Shin sagometer data and particle analysis; V.A.S. capsule physics; B.K.S. ensemble simulations; P.T.S. dynamic model, ignition theory; M.S. capsules; S. Stoupin X-ray diagnostics; D. J. Strozzi hohlraum/LPI physics; L.J.S. hohlraum physics; C.A.T. Bigfoot design physics; R.P.J.T. programme management; E.R.T. optical diagnostics; P.L.V. neutron imaging diagnostics; C.R.W. capsule/instability physics; K.W. X-ray diagnostics; C.W. capsule fabrication; C.H.W. neutron diagnostics; B.M.V.W. NIF operations lead; D.T.W. hohlraum physics; B.N.W. project engineering; M.Y. capsule fabrication; S.T.Y. MOR and PAM stability, SSD improvements and FC control; G.B.Z. computational physics lead.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review information
Nature thanks Shinsuke Fujioka, Erik Lefebvre and Nigel Woolsey for their contribution to the peer review of this work.
Additional information
Extended data
is available for this paper at https://doi.org/10.1038/s41586-021-04281-w.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zylstra, A.B., Hurricane, O.A., Callahan, D.A. et al. Burning plasma achieved in inertial fusion. Nature 601, 542–548 (2022). https://doi.org/10.1038/s41586-021-04281-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-04281-w